I think that computer programming/software development is a process that requires practice in order to maintain skills and get better. That’s why I’m always looking for little projects or katas, little projects that can be done in an hour or two. I found one a while back that I liked so I thought I’d write it up.
The Problem
Implement a diceware password generator. You should read that link for background but as a summary:
Diceware™ is a method for picking passphrases that uses dice to select words at random from a special list called the Diceware Word List. Each word in the list is preceded by a five digit number. All the digits are between one and six, allowing you to use the outcomes of five dice rolls to select a word from the list.
Caveat 
Since we are creating a program that generates a “random” passphrase you might be tempted to actually use it for that purpose. That isn’t necessarily a good idea. This code relies on the random number generator inside a computer. If that random number generator is compromised somehow (and how would we know if it were?), the passphrase generated would not be random. This is why the diceware site tells you to roll real, physical dice.
The upshot is this: Don’t use this code to generate real passwords. This is just an exercise.
Call me the Tumblin’ Dice
Let’s start with creating a virtual die. The rand-int function looks promising
user=> (doc rand-int)
-------------------------
clojure.core/rand-int
([n])
Returns a random integer between 0 (inclusive) and n (exclusive).
So a 6 sided die roll would look something like this
(defn roll-die []
(inc (rand-int 6)))
Try it!
user=> (roll-die)
1
user=> (roll-die)
1
user=> (roll-die)
2
user=> (roll-die)
6
How do we know it works? We can’t know for sure but we can gain some confidence by using the REPL
user=> (frequencies (repeatedly 6666 roll-die))
{2 1126, 6 1103, 4 1097, 1 1120, 3 1117, 5 1103}
The repeatedly call returns a sequence of calls to our function. In this case we’re creating a sequence of 6666 calls. The frequencies call returns a map where each key is a result and its value is how many times it occurred in the input sequence. We would expect a proper 6-sided die to have each number come up around 1111 times.
As you can see from the return value of the REPL call, we have 6 entries and each has a value around 1111. This is good enough, we can proceed.
Generate the Key
We need a function that rolls our die 5 times and creates a 5 digit number from the results. We saw just above that we can use repeatedly to create a sequence of rolls
user=> (repeatedly 5 roll-die)
(4 3 1 2 6)
That’s good but how do we make a number out of that? There’s a lot of ways we could do it but this is kind of a fun way that relies on the fact that:
43126 = 4 x 10^4 + 3 x 10^3 + 1 x 10^2 + 2 x 10^1 + 6 x 10^0
or, if you prefer math notation
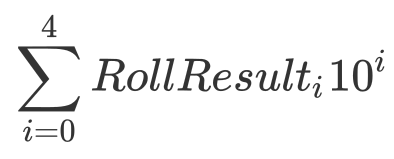
Let’s write that out in clojure and then we’ll discuss
(defn generate-key []
(let [roll-results (repeatedly roll-die)
exponents (map (fn [n] (int (Math/pow 10 n)))
(reverse (range 0 5)))]
(reduce + (map * roll-results exponents))))
There’s a lot there so let’s break it apart.
First we create a roll-results sequence. We don’t bother supplying a number parameter to the repeatedly call so this actually represents an infinite sequence of die rolls. Crazy, eh? Don’t worry though, it is lazily evaluated.
Next we make an exponents sequence. It is a map across the sequence (reverse (range 0 5)). That sequence looks like
(4 3 2 1 0)
The map function is just a call to the java static method Math.pow(). We supply the exponent 10 so that the result is this
(10000 1000 100 10 1)
Now, the (map * roll-results exponents) works like a vector product multiplying each number in our roll-results sequence against the exponents sequence producing a sequence of multiplied numbers. When map is called with multiple sequences like this it will only produce a sequence that is the size of the smaller of the input sequences. Our exponents sequence is 5 elements long so the resulting sequence will be 5 elements long too even though the roll-results sequence is infinite.
Finally, to add up all the multiplied numbers we use the reduce + call resulting in a single 5-digit integer.
Let’s try it
user=> (generate-key)
65152
user=> (generate-key)
34342
user=> (generate-key)
62536
Yeah! So we now can generate a random number representing a 5 dice rolls. Next we need to use that to look up our passphrase words. We will handle that task in a next installment. Let’s end just by showing you the code written so far
(defn roll-die []
(inc (rand-int 6)))
(defn generate-key []
(let [roll-results (repeatedly roll-die)
exponents (map (fn [n] (int (Math/pow 10 n)))
(reverse (range 0 5)))]
(reduce + (map * roll-results exponents))))
That’s it!